SYMÉTRIE (physique)

SYMÉTRIE (physique)

La notion de symétrie en physique est assez intuitive; elle n’a été formalisée et généralisée que depuis moins d’un siècle: en plus des symétries spatio-temporelles, il en existe d’autres, liées à des concepts physiques plus abstraits tels que l’indiscernabilité des particules ou l’isospin. Les considérations de symétrie sont en général appliquées aux états physiques, mais on étudiera aussi sous ce terme l’ensemble des transformations qui laissent invariantes les lois de la physique. Cet ensemble est un groupe (cf. GROUPES [mathématiques]) que l’on appellera groupe d’invariance. Les équations de la physique sont invariantes par ce groupe, en ce sens qu’elles gardent la même forme par les transformations de ce dernier.

Cette dernière notion est assez abstraite. Elle a été peu à peu établie en partant de l’étude de la symétrie des états physiques, pour aboutir enfin à celle des lois de la physique. C’est Pierre Curie qui, l’un des premiers, fit une étude systématique des symétries des états physiques. Citons deux phrases caractéristiques de son article «Sur la symétrie des phénomènes physiques» (Journal de physique , 3^e série, t. III, 1894): «Lorsque certaines causes produisent certains effets, les éléments de symétries des causes doivent se retrouver dans les effets produits», et: «Lorsque certains effets révèlent une certaine dissymétrie, cette dissymétrie doit se retrouver dans les causes qui lui ont donné naissance.»

Voyons sur un exemple très simple comment on distingue la symétrie d’un état physique de celle des lois de la physique: s’il n’y a pas de vent, toutes les directions horizontales sont équivalentes pour un athlète lançant le poids, mais la direction verticale a un rôle privilégié; cela n’est pas dû à une dissymétrie des lois de la physique, mais à ce que l’athlète considéré a les pieds sur la Terre, et son environnement est ainsi dissymétrique. Qu’il se transforme en cosmonaute, isolé dans l’espace, toutes les directions lui deviendront équivalentes, et le poids lancé s’éloignera en ligne droite à vitesse constante.

1. Groupe connexe d’invariance géométrique de la physique

Dans l’étude du groupe connexe d’invariance géométrique de la physique, le mot «connexe» signifie qu’on ne s’occupe ici que des transformations qui se déduisent continûment de la transformation identité.

Invariance euclidienne

L’invariance euclidienne est l’invariance par le groupe des déplacements euclidiens. Ce groupe est engendré par les translations et les rotations dans l’espace à trois dimensions; l’invariance par translations et rotations traduit respectivement l’homogénéité et l’isotropie de cet espace. Les éléments du groupe euclidien sont fixés par six paramètres: trois pour la translation, deux pour la direction de l’axe de rotation et un pour l’angle de rotation.

L’équation fondamentale de la dynamique newtonienne:

où f est la force, 塚 l’accélération, v la vitesse et m la masse, est bien invariante par les changements de coordonnées correspondant à des rotations (les deux vecteurs f et 塚 restant colinéaires) ou à des translations rr 漣 a; en effet, on a:

Invariance temporelle

L’équation (1) est aussi invariante par translation dans le temps:

Il semble raisonnable de supposer que les lois de la physique ne se modifient pas au cours du temps. Il est vrai que des physiciens avaient pu admettre que des constantes universelles, celle de la gravitation par exemple, avaient changé au cours du temps. Si l’on acceptait généralement ce point de vue, c’est que, probablement, cette «constante» serait devenue un nouveau champ. Les translations de temps ajoutent un septième paramètre au groupe euclidien E.

Invariance galiléenne

L’équation (1) est encore invariante par les transformations galiléennes:

qui dépendent de trois paramètres. Cela traduit l’hypothèse de Galilée: «Les lois de la mécanique sont les mêmes pour deux observateurs en mouvement uniforme (c’est-à-dire pour v⁰ constante) l’un par rapport à l’autre.» Il n’y a pas de repos absolu dans l’espace vide.

Invariance relativiste

Les équations de Maxwell (cf. ÉLECTRICITÉ - Électromagnétisme, chap. 2), qui depuis plus de cent ans forment les fondements de l’électromagnétisme, ne sont pas invariantes par les transformations galiléennes; elles se trouvent donc en conflit avec les lois de la mécanique, comme on s’en aperçut à la fin du XIX^e siècle. En 1904, Lorentz montra (cf. ESPACE-TEMPS, chap. 3) par quelles transformations devaient être remplacées les transformations (3):

où c est la vitesse de la lumière dans le vide (environ 300 000 km/s) et: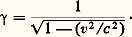

En 1905, Poincaré montra que les transformations de Lorentz, avec les translations d’espace et de temps et les rotations, forment un groupe que nous dénotons par P⁰. La même année, Einstein, par la théorie de la relativité restreinte, transforme la dynamique qui devient aussi invariante par P⁰. La dynamique newtonienne n’est qu’une approximation de la dynamique relativiste valable pour les vitesses faibles par rapport à c .

2. Invariance et lois de conservation

La physique relativiste est-elle identique pour des observateurs «équivalents», c’est-à-dire pour des observateurs dont les systèmes de référence sont en mouvement uniforme l’un par rapport à l’autre?

Invariance passive et invariance active

Pour mieux comprendre les relations entre les grandeurs physiques et le groupe d’invariance de la physique, on considérera aussi la restriction de ces relations à un sous-groupe G de P⁰ que l’on appellera groupe de relativité. Si par exemple G est le groupe euclidien, les observateurs équivalents se déplacent mais ils sont en repos, les uns par rapport aux autres.

On appelle invariance passive le postulat suivant lequel les lois physiques et les équations qui les traduisent s’expriment de la même façon dans les repères (c’est-à-dire les systèmes de coordonnées d’espace et de temps) des différents observateurs équivalents. Il s’agit au contraire d’invariance active lorsqu’on considère simultanément un système physique S et son transformé g 練 S = S par une transformation arbitraire g , du groupe de relativité G. Cette invariance exige que la description de S dans un repère R et la description de S dans le repère équivalent R = g 練 R, transformé de R par la même opération g , soient identiques et le restent au cours de l’évolution de ces deux systèmes.

Comme on ne sait pas changer les grandeurs intrinsèques attachées aux atomes, les changements d’échelle de la masse, des coordonnées d’espace et de temps, etc., permettent d’étudier la seule invariance passive, ce qui est exploité par l’analyse dimensionnelle.

Un même système physique est vu par divers observateurs équivalents sous des états différents, comme diverses personnes voient le même objet sous différents points de vue. Elles reconnaissent qu’il s’agit du même objet en échangeant entre elles des informations en termes d’«invariants» du groupe de relativité G et en constatant que ce sont les mêmes: par exemple, les dimensions de l’objet sont des invariants du groupe des déplacements euclidiens.

Invariants et covariants

Les grandeurs physiques qui décrivent l’état d’un système ne sont pas les mêmes pour différents observateurs équivalents, mais elles doivent se transformer suivant des lois précises par le groupe G: ce sont des covariants de G. Par exemple, si G est le groupe des rotations, l’impulsion p et le moment cinétique J se transforment comme un vecteur, tandis que l’énergie E est invariante. Pour le groupe de Poincaré P⁰ lui-même, l’impulsion et l’énergie forment les quatre composantes d’un vecteur impulsion-énergie, invariant par les translations, tandis que J représente trois des six composantes d’un tenseur antisymétrique.

Plus généralement, les états d’un système sont eux-mêmes des covariants de G; en mécanique quantique, le groupe G les transforme linéairement entre eux. C’est pourquoi les applications de la théorie des groupes ont été beaucoup plus développées en mécanique quantique (cf. bibliographie).

Comme on l’a vu, ce sont les grandeurs physiques invariantes par G qui permettent de caractériser un système physique. Les systèmes «élémentaires» seront déterminés par un nombre minimal d’invariants; on les appelle particules élémentaires, en attendant de leur trouver une structure plus complexe. En mécanique quantique, l’espace des états d’une particule élémentaire devra donc former une représentation (linéaire) irréductible de P⁰; il ne possède alors que deux invariants pour ce groupe, sa masse:

et son spin (ou moment cinétique intrinsèque). Les valeurs possibles du spin sont des multiples entiers ou demi-entiers positifs (c’est-à-dire 0, 1/2, 1, 3/2, ...) de 寮 = h /2 神, où h désigne la constante de Planck (face=F0019 寮 = 1,054 59 憐 10^-27 erg 練 s) [cf. SPIN].

Lois de conservation

Dans l’invariance active, la description de S dans le repère R et celle de S dans R ne peuvent rester identiques au cours de leur évolution que si les grandeurs physiques qui mesurent leur état sont également conservées. Dans toute théorie physique, l’invariance par un groupe G implique des lois de conservation. Lorsque G est un groupe de Lie, connexe de n paramètres, il y a n lois de conservation correspondantes: pour les trois translations d’espace, les trois composantes de l’impulsion; pour la translation temporelle, l’énergie; pour les rotations (trois paramètres), les trois composantes du moment cinétique; pour les transformations de Lorentz, trois autres composantes qui, avec celles du moment cinétique, forment un tenseur du second rang antisymétrique.

Ces lois de conservation ne s’appliquent qu’aux systèmes physiques isolés. Si un système physique est modifié au cours du temps, par une interaction avec l’extérieur, il n’est pas invariant par translation temporelle et son énergie n’est pas conservée: il échange de l’énergie avec l’extérieur. Seule l’énergie totale (système et extérieur) est conservée. Il faut donc bien distinguer entre le groupe de symétrie du système et celui des lois physiques. En général, le premier est plus petit; mais, comme nous allons le voir pour la violation de la parité, le premier peut contenir des transformations qui ne sont pas dans le deuxième. Dans ce cas, un système isolé pourra perdre spontanément une partie de sa symétrie, contrairement au principe de Curie (cf. supra ).

3. Invariances discrètes géométriques

Parité P

La réflexion dans un miroir est une visualisation de la symétrie par rapport à un plan (ici, celui du miroir): l’image de notre main droite est la main gauche de notre image dans le miroir. Si les lois de la physique sont invariantes par symétrie plane, on ne peut distinguer un phénomène physique de son «image miroir», et les seules lois physiques ne nous permettront pas de définir la gauche et la droite. On a pourtant enseigné le contraire avec le «bonhomme d’Ampère», le tire-bouchon de Maxwell ou la règle des trois doigts (de la main droite!), en représentant le champ magnétique par un vecteur. Curie (op. cit. ), cependant, signalait déjà en 1894 que «cette représentation est défectueuse au point de vue spécial de la symétrie». La figure 1 a montre comment un vecteur (un champ électrique E, une vitesse v, etc.) est transformé par une symétrie par rapport à un plan horizontal. La composante horizontale (fig. 1) reste invariante tandis que la composante verticale change de signe. La même symétrie ne modifie donc pas le courant électrique d’une boucle de circuit horizontal où le champ magnétique résultant, qui est vertical, est inchangé (fig. 1 b). Inversement, la même symétrie change le sens de parcours d’un courant électrique dans un fil conducteur vertical, et le champ magnétique qu’il produit, qui est horizontal, est changé de signe par la symétrie. Il faut donc représenter un champ magnétique non par un vecteur, mais par un pseudo-vecteur sur qui une symétrie produit un changement de signe supplémentaire à la transformation d’un vecteur; au lieu de pseudo-vecteur, on dit aussi vecteur axial (cf. ÉLECTRICITÉ - Électromagnétisme, chap. 3), le vecteur ordinaire étant appelé «vecteur polaire».

Les phénomènes électromagnétiques, ainsi que les interactions nucléaires (dites encore «fortes») et gravitationnelles, sont bien invariants par les symétries planes. Comme nous l’avons vu, à toute invariance correspond une loi de conservation. Les physiciens appellent parité la quantité physique conservée par l’invariance par symétrie plane. Il existe un quatrième type de forces dans les phénomènes physiques, les interactions de Fermi (1934), responsables de la radioactivité 廓 par exemple ^{[cf. RADIOACTIVITÉ]}, et qualifiées aussi de «faibles» parce qu’elles sont 10¹⁰ fois plus faibles que les interactions électromagnétiques (les interactions gravitationnelles sont 10³⁶ fois plus faibles que les interactions électromagnétiques, mais ces deux seules interactions ont une portée macroscopique). T. D. Lee et C. N. Yang proposèrent la violation de la parité par les interactions de Fermi pour résoudre des contradictions apparentes dans les résultats expérimentaux sur la désintégration des mésons K ^{[cf. PARTICULES ÉLÉMENTAIRES]}. Il est, depuis lors, bien établi que les interactions de Fermi ne sont pas invariantes par les symétries planes. La première confirmation expérimentale intervint quelques mois après la prédiction de Lee et de Yang; elle fut réalisée indépendamment par trois groupes de physiciens américains: R. L. Garwin, L. M. Lederman, M. Weinrich d’une part et J. I. Friedmann, V. L. Telegdi d’autre part étudièrent la désintégration des leptons 猪⁺ polarisés, tandis que C. S. Wu, E. Ambler, R. W. Hayward, D. D. Hoppes, R. P. Hudson se penchèrent sur celle du cobalt 60.

La figure 2 montre schématiquement la première expérience: on observe au repos des leptons 猪⁺ polarisés. Cette polarisation s (verticale et dirigée vers le haut dans la figure) est obtenue naturellement pour les 猪⁺ provenant de la désintégration des mésons 神⁺; elle est parallèle au champ magnétique B et, comme lui, elle est un pseudo-vecteur (cf. SPIN, chap. 4). Le plan horizontal est donc un plan de symétrie des 猪⁺ polarisés. Les 猪⁺ se désintègrent, avec une vie moyenne de 2 練 10^-6 seconde, en un électron positif (e ⁺ = positron) et deux neutrinos. Or la distribution angulaire des positrons produits n’est pas symétrique par rapport au plan horizontal; elle est proportionnelle à:

étant l’angle entre s et v, la vitesse de l’électron. Par exemple, dans la direction verticale, le nombre de positrons émis vers le bas est donc les sept cinquièmes du nombre de ceux qui sont émis vers le haut. Le plan horizontal est le plan de symétrie de l’état initial de l’expérience; il ne l’est plus après la désintégration des 猪⁺. La cause de cette perte de symétrie est la non-invariance des interactions de Fermi par rapport aux symétries planes.

Renversement du temps T

L’invariance par renversement du temps, considérée aussi dès la fin du XIX^e siècle, devrait proprement être appelée «renversement du mouvement». Si, à un instant donné t ⁰, pris comme origine des temps (t ⁰ = 0), les vitesses de chaque astre du système solaire (Soleil, planètes et leurs satellites) étaient renversées, leur trajectoire ne serait pas modifiée, mais la position de chaque astre sur sa trajectoire à l’instant ultérieur t serait celle qu’il occupait à l’instant 漣 t . On pourrait alors faire les nouveaux éphémérides à partir des anciens, simplement en «renversant le temps». Jusqu’en 1964 (cf. Invariance CPT , in chap. 5), aucun phénomène physique actuellement connu n’a permis de mettre en doute le fait que les quatre types d’interaction déjà mentionnés (nucléaire ou forte, électromagnétique, de Fermi ou faible, gravitationnelle) ne seraient pas invariants par T. Il est vrai que la plupart des phénomènes macroscopiques (tels que frottement, dissipation) sont «irréversibles»; mais cela est bien expliqué par la mécanique statistique ^{[cf. THERMODYNAMIQUE]} appliquée aux systèmes composés d’un grand nombre de constituants (le nombre d’Avogadro est égal à 6 練 10²³).

4. Relativité générale et cosmologie

En prolongeant ses réflexions sur la relativité qu’on appelle maintenant «restreinte», Einstein fut amené à postuler une nouvelle forme d’invariance pour la gravitation. Dans un véhicule en mouvement accéléré, par exemple, la surface d’un liquide n’est plus horizontale. Le même effet pourrait être obtenu par une redistribution des masses dans l’Univers: il y a «équivalence» entre forces de gravitation et accélération. Les accélérations sont des transformations «actives». L’article RELATIVITÉ explique comment Einstein fut conduit à la relativité générale, ultime formulation de la théorie de la gravitation. Dans cette théorie, l’invariance par P⁰ n’y est qu’approchée: en effet, notre espace-temps n’est plus un espace affine (cf. algèbre LINÉAIRE ET MULTILINÉAIRE) mais une variété ^{[cf. VARIÉTÉS DIFFÉRENTIABLES]} dont la connexion dépend en chaque point du tenseur impulsion-énergie. Grosso modo, la forme de l’espace-temps dépend de la répartition de la matière qu’il contient ^{[cf. ESPACE-TEMPS]}. Seule l’action du groupe de Lorentz (engendré par les rotations et les transformations de Lorentz) reste bien définie en chaque point de l’espace-temps; les translations d’espace et de temps ne le sont plus. Le groupe des transformations passives contient toutes les transformations différentiables des coordonnées d’espace-temps.

Des variantes sont encore possibles dans la formulation de cette théorie de la gravitation, entre lesquelles de nouvelles expériences (entre autres, les expériences faites avec des satellites artificiels) nous permettront probablement de choisir.

Il ne faut pas confondre la relativité générale avec la cosmologie, dont l’objet est l’étude de l’Univers ^{[cf. COSMOLOGIE]}. Le terme «Univers» désigne l’ensemble de la matière avec laquelle il est possible d’interagir, grâce essentiellement aux interactions gravitationnelles et électromagnétiques, les deux autres interactions, «fortes» et «faibles», n’étant pas de longue portée. Dans l’état actuel de nos connaissances, notre Univers n’est invariant ni par translation du temps ni par translation d’espace, c’est-à-dire ni immuable ni homogène. En effet, sa taille est limitée à quelques milliards d’années de lumière; il est en expansion et il semble bien qu’il soit passé, il y a presque vingt milliards d’années, par un état très condensé, très fugitif, sujet d’études passionnées. Comme résidu de cet état initial (big bang en anglais), on peut, entre autres choses, observer une distribution de rayonnement électromagnétique, à la température de 2,7 K, baignant tout l’Univers, prédite par G. Gamov vingt ans avant sa découverte en 1968. Ce rayonnement définit un repère absolu dans l’Univers, et l’on a mesuré (par effet Doppler) la vitesse de la Terre par rapport à lui.

Cela nous montre que les symétries des lois de la physique n’ont été exprimées qu’en faisant abstraction de toutes les dissymétries de l’environnement, et cela même à l’échelle de l’Univers.

5. Invariances dynamiques

Nous désignons par invariances dynamiques les invariances non reliées à l’espace-temps mais inscrites dans les équations fondamentales de la physique. Il ne s’agit pas seulement d’une invariance syntactique du formalisme mathématique de la théorie physique, comme un exemple nous en est donné en thermodynamique classique; toutes ses équations sont invariantes par les permutations simultanées:

ou encore:

où F et G sont respectivement l’énergie libre de Helmholtz et celle de Gibbs, H l’enthalpie, U l’énergie interne, S l’entropie, P la pression, V le volume, T la température.

Depuis dix ans environ, nos vues sur la symétrie interne des équations de la physique se sont approfondies. Mais, si nous comprenons bien les invariances dynamiques exactes, nous ne pouvons encore en dire autant des invariances approchées.

Invariance par permutation de particules identiques

Par définition de l’identité, le formalisme permettant d’étudier un ensemble E de systèmes physiques identiques (molécules, par exemple) doit les considérer de manière complètement symétrique. Pour ces systèmes identiques, on utilisera ci-dessous le terme général de particules. Puisqu’en mécanique classique on peut suivre l’évolution individuelle (la trajectoire, par exemple) des particules, on obtient par une permutation de celles-ci un autre état de E, et en général il n’y a pas d’évolution possible d’un état de E à l’état permuté. En mécanique quantique, au contraire, il n’est plus possible de suivre individuellement chaque particule d’un ensemble E de particules identiques; aussi, pour tout état de E, toute permutation des particules redonne le même état. Les particules de E sont indiscernables, et tout observable de E est une fonction complètement symétrique (c’est-à-dire invariante par toute permutation) des observables des particules. Comme les observables d’un état sont des fonctions quadratiques de sa fonction d’onde, il faut considérer deux cas: la fonction d’onde est soit complètement symétrique dans les coordonnées de particules, soit complètement antisymétrique (c’est-à-dire invariante pour les permutations paires et changeant de signe pour les permutations impaires). On dit que les particules suivent la statistique de Bose dans le premier cas, et la statistique de Fermi dans le second. Les particules de spin entier sont des bosons (c’est-à-dire qu’elles suivent la statistique de Bose) et les particules de spin demi-entier sont des fermions. Cette relation entre spin et statistique ^{[cf. SPIN]} est partie intégrante de la théorie quantique et relativiste des champs, comme l’a montré W. Pauli (1940). Le type de la statistique est toujours conservé par permutation des particules.

Invariance de jauge

Les charges conservées correspondent-elles à une invariance? Il est remarquable que ces charges ne puissent prendre que des valeurs qui sont des multiples entiers d’une charge élémentaire; cela s’explique par leur conservation et la constitution de la matière en particules. En mécanique quantique, il est toujours possible (et souvent nécessaire) de rendre complexe la fonction d’onde 切 d’un état; mais la valeur de la charge de cet état n’est fonction que de 切切 漣 = | 切|², carré du module de 切, et donc indépendante de sa phase. Le formalisme est invariant par 切切 e ⁱ size=1^見q , où q est la valeur (entière) de la charge de l’état décrit par 切 et 見 une constante; l’ensemble de ces multiplications par une phase complexe forme un groupe qui est souvent appelé U(1), le groupe U(n ) étant le groupe des matrices unitaires n 憐 n . Combien existe-t-il de charges dans la nature, en plus de la charge électrique, qui peuvent être portées par les «particules élémentaires»? ^{[cf. PARTICULES ÉLÉMENTAIRES]}. En dehors du photon, le quantum des interactions électromagnétiques, ces particules se répartissent en deux grands groupes: les hadrons qui ont des interactions nucléaires (on dit encore «fortes») et les leptons qui n’en ont pas; toutes ces particules sont en interactions «faibles» (on dit parfois de Fermi, le premier physicien qui proposa une théorie de ces forces responsables, par exemple, de la désintégration spontanée des noyaux). Les hadrons qui satisfont à la statistique de Fermi sont appelés baryons et ils portent une charge élémentaire baryonique (négative pour les antiparticules) tandis que les mésons (hadrons satisfaisant à la statistique de Bose), qui jouent le rôle de quanta des interactions fortes, ne portent pas de charge baryonique. Le noyau des atomes est constitué de protons, p , et de neutrons, n : ce sont des baryons. Tous les autres hadrons sont donc des particules très fugitives (vie moyenne comprise entre 10^-8 et 10^-23 seconde), plusieurs types étant découverts entre 1947 et 1960 (mésons 神⁺, 神⁰, 神^-, K⁺, K⁰, K 漣⁰, K^-, baryons 炙⁰, ⁺, ⁰, ^-, 輻^-, 輻⁰ et les antibaryons correspondants, les antiprotons et antineutrons n’ayant été observés eux-mêmes qu’en 1955 et 1957). Depuis lors ont été produits, dans les grands accélérateurs, plusieurs centaines de types de hadrons. Les leptons sont des fermions avec une charge leptonique l pour les particules, 漣 l pour les antiparticules. L’électron e ^- (constituant des atomes) et son antiparticule e ⁺ le positron sont les seuls leptons chargés électriquement et stables. Il leur est associé un neutrino 益^e et son antineutrino 益^e , tous deux électriquement neutres, de masse probablement nulle, et qui ont été postulés par Pauli en 1931. Ces neutrinos sont émis spontanément dans les désintégrations 廓 des noyaux atomiques par exemple, ou sont produits par les réactions nucléaires au cœur des étoiles (nous en recevons du soleil de l’ordre de 10¹¹ 益^e par seconde et par centimètre carré; tous sauf un en moyenne traversent la terre sans interagir). Les deux autres familles de leptons connues sont les 猪^-, 猪⁺ et leurs neutrinos associés 益 size=1^猪, 益 size=1^猪. Les 猪 furent observés avant 1940 dans les rayons cosmiques et confondus au début avec le méson prédit par Yukawa en 1935 et qui fut découvert en 1947 sous sa forme chargée ( 神⁺, 神^-). C’est en 1960 qu’on établit que le neutrino 益 size=1^猪 associé au 猪 et le neutrino 益^e associé à l’électron étaient différents. En 1975, on découvrit les 精^-, 精⁺ et leurs neutrinos (probablement) associés 益 size=1^精, 益 size=1^精. On a découvert en 1983, au C.E.R.N. (Genève), les quanta des interactions faibles W⁺, W^-, Z⁰ extrêmement lourds (leur masse est comparable à celle d’un atome de krypton et de molybdène); ils n’ont pas de charge leptonique.

Enfin, toutes les particules interagissent avec le champ de gravitation (dont le quantum, hypothétique, est appelé graviton et aurait un spin 2 寮); mais il n’existe pas de charge quantifiée correspondant à la gravitation, puisque c’est la masse (ou plus exactement le tenseur impulsion-énergie) qui fixe l’intensité de l’interaction gravitationnelle pour chaque particule.

En mécanique quantique, la valeur d’une grandeur physique pour un état donné ne peut généralement être prédite que de façon probabiliste. G. C. Wick, A. S. Wightman et E. P. Wigner (1952) ont montré l’existence de grandeurs physiques ayant la propriété de supersélection, c’est-à-dire que, pour tout état physique, leurs valeurs sont certaines. C’est le cas des grandeurs conservées: type de statistique, charges b , l , q qui correspondent aux invariances dynamiques absolues que nous venons d’étudier.

Conjugaison de charge C

L’invariance par conjugaison de charge C ne fut prédite qu’en 1931 par J. R. Oppenheimer et P. A. M. Dirac. L’étude de l’équation qu’il avait inventée amena celui-ci à prédire l’existence de l’antimatière, c’est-à-dire les antiparticules de celles qui étaient connues alors: l’anti-électron e ⁺ (ou positron) découvert l’année suivante et l’antiproton p ^- découvert en 1955. En même temps, il prédisait leur propriété puisque cette conjugaison C associe à toute particule une antiparticule de même masse, de même spin, mais de charges opposées (il s’agit des charges baryonique, électrique, leptonique). Une particule est l’antiparticule de sa conjuguée, à moins qu’elle ne soit sa propre conjuguée, ce qui est le cas des photons ( 塚) et des mésons neutres sans «étrangeté» ^{[cf. PARTICULES ÉLÉMENTAIRES]}. On peut attribuer à ces particules self-conjuguées de charge une nouvelle grandeur physique c , de valeur 梁 1, conservée par C: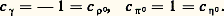

Dans le langage courant, on réserve le nom de particule au proton positif (p ⁺), à l’électron négatif (e ^-), etc., parce que l’Univers autour de nous est dissymétrique par C. Existe-t-il dans d’autres parties de l’Univers des galaxies d’antimatière? Les émissions électromagnétiques ne permettent pas de distinguer matière et antimatière, et l’annihilation en mésons et en photons de la matière et de l’antimatière n’a pas été observée à grande échelle dans l’Univers ^{[cf. ANTIMATIÈRE]}.

Actuellement, il semble bien que C soit une invariance des trois interactions forte, électromagnétique et de gravitation, mais elle est violée par les interactions de Fermi. Bien que la nature ne nous fournisse pas aussi facilement des leptons 猪^- au repos complètement polarisés, le coefficient a ^- d’asymétrie de leur désintégration n’est pas égal à a ⁺ (équation 5) mais à son opposé:

Cette relation montre, inversement, que les interactions de Fermi sont invariantes pour le produit PC ou CP des symétries P et C.

Invariance CPT

Dans l’article PARTICULES ÉLÉMENTAIRES (chap. 4), on indique qu’en 1964 un nouveau type d’interaction (un cinquième?) fut observé dans la désintégration des mésons K⁰ qui ne respecte pas l’invariance CP. Il semble établi maintenant qu’elle viole aussi l’invariance T, tout en respectant le produit CPT. Dès 1954, J. Bell, G. Lüders, W. Pauli, J. Schwinger avaient montré que l’invariance CPT est plus fondamentale que les invariances C, P, T séparées. Si un phénomène physique la violait, il serait en conflit aigu avec toutes les théories actuelles de la physique fondées sur la théorie quantique des champs et sur la notion de causalité.

On voit donc apparaître des relations profondes entre des invariances géométriques P, T, qui ne sont qu’approchées, et une invariance dynamique C, elle aussi seulement approchée. Nous allons maintenant traiter des autres symétries dynamiques approchées.

Symétries internes des particules

On désigne par symétries internes des particules les invariances dynamiques approchées des lois physiques, car elles correspondent à des groupes de transformation sur les coordonnées «internes» des particules élémentaires; ce sont des coordonnées que l’on doit rajouter aux coordonnées d’espace, de temps et de spin. La conjugaison de charge C est en fait un premier exemple de telles symétries.

Protons et neutrons sont les constituants des noyaux atomiques. Lorsqu’on néglige leur différence, on ne peut plus les distinguer les uns des autres. Ce n’est pas une boutade. Le fonctionnement de nos appareils de détection de particules est toujours fondé en partie au moins sur des phénomènes électromagnétiques puisque ces interactions sont les seules, avec la gravitation, à avoir une portée macroscopique (mais la gravitation est négligeable à l’échelle d’une particule). L’observation des protons, qui ont une charge électrique + e , et des neutrons, qui n’ont pas de charge électrique, se fait donc par des moyens très différents. Malgré cela, les physiciens ont découvert la profonde similitude entre protons et neutrons: leur masse est égale, à un millième près, ils ont le même spin, la même charge baryonique et leur différence est purement de nature électromagnétique; enfin, du point de vue des interactions nucléaires, ils sont identiques. Dès la découverte du neutron (1932), Heisenberg proposa de traiter proton et neutron comme deux états p et n de la même particule, le nucléon; plus précisément, p et n sont les deux valeurs de la «coordonnée interne» du nucléon, qui identifient des particules indiscernables lorsqu’on ne s’occupe que des interactions nucléaires. Les nucléons sont des fermions. Il y a isomorphisme mathématique entre le traitement de la coordonnée de spin et celui de la coordonnée interne du nucléon, car elles prennent chacune deux valeurs. Par analogie, on a donc appelé isospin la quantité conservée, qui est fonction de la coordonnée interne; l’isospin du nucléon est 1/2. D’autre part, grâce aux relations profondes entre les représentations linéaires des groupes de permutation et celles des groupes linéaires ou unitaires (cf. GROUPES [mathématiques]), on peut décrire de façon équivalente la conservation de l’isospin dans les interactions nucléaires par l’action du groupe SU(2) agissant sur la coordonnée interne des nucléons (SU(n ) est le sous-groupe de U(n ) formé par les matrices unitaires de déterminant 1).

Bien que ce soit à une approximation plus grossière près, les forces nucléaires ne distinguent pas non plus entre spin et isospin; il n’est donc pas simplement formel de confondre ces deux types de coordonnées en une seule, sur qui agit le groupe SU(4). Cette invariance fut introduite par Wigner en 1937.

La symétrie SU(2), responsable de la conservation de l’isospin, bien qu’approchée, s’est révélée extrêmement féconde ^{[cf. PARTICULES ÉLÉMENTAIRES]}. Avec les neutrons et protons, d’autres baryons furent découverts dans les années cinquante (cf. supra : 炙⁰, ^-, ⁰, ⁺, 輻^-, 輻⁰, ^-, ⁰, ⁺, ⁺⁺) et depuis 1960. On recense actuellement presque deux cents baryons qui se groupent en multiplets de 2, 3, 4 particules correspondant à la valeur 0, 1/2, 1, 3/2 de l’isospin. À chacun de ces baryons doit correspondre sa propre antiparticule antibaryon). De même, les mésons 神 et K (cf. supra ) sont maintenant accompagnés de plus de cent autres mésons. Les tables Review of particle properties qui regroupent toutes les particules connues paraissent tous les deux ans et s’allongent rapidement. Ces mésons sont soit isolés (comme 猪⁰, 諸⁰), soit ils se groupent en doublets d’isospin auxquels s’ajoute le doublet d’antiparticules correspondantes (par ex. K⁰K⁺ et K 漣⁰K^-), soit en triplets ( 神^- 神⁰ 神⁺, 福^- 福⁰ 福⁺). Les multiplets mésoniques d’isospin sont transformés en eux-mêmes par la conjugaison de charge C, ce qui a conduit à leur attribuer un nouveau nombre quantique (L. Michel, 1953), l’isoparité g, quantité conservée par les interactions nucléaires (g size=1^神 = g size=1^諸 = 1, g size=1^福 = g size=1^兀 = 1).

Comme on l’indique dans l’article PARTICULES ÉLÉMENTAIRES, M. Gell-Mann et Y. Ne’eman, ainsi que D. Speiser et J. Tarski, en 1961, ont groupé les multiplets de hadrons (les baryons d’une part et les mésons d’autre part) en multiplets plus grands correspondant au groupe SU(3), ce qui permit de prévoir, pour remplir des cases manquantes, de nouveaux hadrons, découverts depuis lors. On appelle spin unitaire la grandeur physique conservée par cette invariance. F. Gursey et L. Radicati, et indépendamment B. Sakita, en 1964, en généralisant à SU(3) le passage de SU(2) à SU(4) fait par E. Wigner, introduisirent l’invariance SU(6). Avec leurs états de spin, l’octet et le décuplet de baryons ^{[cf. PARTICULES ÉLÉMENTAIRES]} forment un «supermultiplet» de cinquante-six états, tandis que les octets de mésons des tableaux 2 et 3 du même article, avec le méson 﨏⁰, forment un «supermultiplet» de trente-cinq états sur lesquels agit la représentation adjointe de SU(6).

Les quarks

Pour simplifier cette classification, M. Gell-Mann et S. Zweig proposèrent indépendamment l’existence de quarks de spin 寮/2 et de charge électrique 2/3 et 漣 1/3 comme constituants des hadrons: les baryons sont formés de 3 quarks, les mésons d’un quark et d’un antiquark. La classification donnée au paragraphe précédent pouvait être comprise en postulant trois types de quarks appelés u , d , s par M. Gell-Mann. Par exemple, p =u , u , d, n =u , d , d, 炙⁰ =u , d , s, 神⁺ =u , 陋, K⁰ =d , 丹, etc. Dès 1968, on acquit des preuves expérimentales de la structure en quarks du proton et du neutron. Mais il a été impossible jusqu’à aujourd’hui d’extraire les quarks ou antiquarks des hadrons. On pense actuellement qu’il s’agit d’une propriété essentielle et nouvelle: les quarks sont «confinés» dans les hadrons et ne pourront jamais en être extraits.

Pour des raisons théoriques, S. Glashow, J. Iliopoulos et L. Maiani prédirent l’existence d’un quark qu’ils notèrent c (pour «charme»); en 1974, le méson c 縷 fut découvert, et en 1978 on découvrit un cinquième type de quark appelé b , encore plus lourd. On en cherche fébrilement au moins un autre baptisé à l’avance «t ». Ces états d , u , s , c , b sont appelés saveur (par esprit de facétie des physiciens).

Vers 1970, encore sous l’impulsion de M. Gell-Mann, et pour préserver la relation entre spin et statistique, fut introduit un nouveau degré de liberté interne des quarks, avec trois états possibles, appelés «couleurs». Cela implique l’existence de huit quanta de masse nulle, les gluons, aussi confinés que les quarks. Les gluons jouent, par rapport à un nouveau type d’interaction, la «chromodynamique», le même rôle que le photon en électrodynamique. Les interactions nucléaires entre nucléons – ou hadrons – sont dérivées de la chromodynamique comme les interactions chimiques découlent de l’interaction électrique entre les électrons d’un atome et son noyau. Les équations fondamentales de la chromodynamique sont les mêmes que celles de l’électrodynamique: les équations de Maxwell et de Dirac, mais en y incluant le degré de liberté interne de couleur; le groupe de jauge U(1) de l’électrodynamique est alors remplacé par le groupe de jauge SU(3) pour la chromodynamique.

6. Brisure spontanée des symétries

Certaines dissymétries apparaissent sans cause apparente. Il s’agit bien d’une violation du principe de Curie cité dans l’introduction. Il ne faut pas le confondre avec le phénomène d’hypersensitivité par rapport aux conditions initiales: si l’on met un crayon verticalement en équilibre sur sa pointe, il finit par tomber horizontalement, en penchant dans une direction impossible à prédire mais qui était en fait déterminée par le défaut infime de verticalité initiale. Bien qu’il s’agisse d’un problème bien déterminé de mécanique des fluides, c’est à cause de cette hypersensibilité aux moindres perturbations que les prédictions météorologiques ne peuvent être valables pour longtemps.

Lorsqu’un problème physique a un groupe de symétrie G, chaque solution n’est pas forcément invariante par G. Si la solution s ne l’est pas, on peut en construire d’autres en utilisant la symétrie G (cf. GROUPES [Mathématiques - Groupes de transformations ]). On obtient ainsi une orbite de G. Seul l’ensemble des solutions est invariant par G. Considérons un ensemble très grand d’atomes: leur interaction deux à deux, ne dépendant que de leur distance, est donc invariante par les translations ou rotations de l’ensemble des atomes, c’est-à-dire pour le groupe euclidien E. À une température donnée, ces atomes en agitation thermique forment un état d’équilibre, par exemple un gaz ou un liquide. C’est un milieu homogène, isotrope de symétrie E. En refroidissant, l’équilibre se déplace et peut devenir un cristal: milieu anisotrope avec des plans privilégiés (plans réticulaires) qui a pour symétrie G, un des 230 groupes cristallographiques (cf. CRISTAUX – Cristallographie). À la transformation liquide-solide, la symétrie est spontanément brisée du groupe euclidien E au sous-groupe G.

Dans notre univers, nous vivons dans un environnement asymétrique; par exemple, nous sommes entourés de matière et non d’antimatière. Il existe peut-être des symétries de lois physiques qui ne sont jamais réalisées dans les états physiques. Comment découvrir ces symétries cachées ? Faisons une comparaison. Supposons que les électrons d’un morceau de cuivre soient intelligents et intéressés par la physique. Ils ont remarqué que leur monde est triplement périodique. Fascinés par les symétries, ils ont même déterminé le groupe cristallographique G du cuivre et qui représente le groupe de symétrie de leur univers. Il leur a fallu faire preuve de pas mal d’abstraction pour trouver cette symétrie car il y a des dislocations locales, leur univers est borné, etc. Résultat, ils connaissent bien le réseau cristallin de leur univers et ses directions privilégiées. Mais seraient-ils assez intelligents pour trouver que les interactions entre les atomes de cuivre sont invariantes par toutes les translations et les rotations (ce qui forme le groupe d’invariance E de la géométrie euclidienne). G n’est qu’un sous-groupe de E. Les «électrons physiciens» découvriraient-ils la symétrie cachée E des lois de la physique?

7. Symétrie cachée des théories physiques

En tout cas, les hommes ont commencé de le faire, il y a dix ans. Une partie de cette symétrie cachée a été trouvée. Nous cherchons actuellement à l’agrandir pour englober toute la physique connue. Les interactions électromagnétiques et faibles sont fort dissemblables. Les premières ont une portée infinie, leur quantum, le photon, ayant une masse nulle, tandis que les quanta de ces dernières, W⁺, W^-, Z⁰, sont extrêmement lourds et ces interactions violent la parité et la conjugaison de charge. À la suite d’une longue chaîne de travaux, dont les plus importants furent ceux de S. Glashow (1962), A. Salam et J. C. Ward (1964), S. Weinberg (1967), G. t’Hooft (1972), on a maintenant une théorie parfaite, très symétrique, basée encore sur les équations de Maxwell et de Dirac, avec une invariance de jauge étendue au groupe U(2). Cette remarquable symétrie de la théorie est toujours spontanément brisée dans notre univers, et elle n’apparaît jamais dans les états physiques. On n’avait jamais vu cela depuis cent ans (lorsque Maxwell unifia électromagnétisme et optique): une unification en une seule théorie de deux parties disjointes de la physique! Cette théorie prédisait non seulement l’existence de W⁺, W^-, Z⁰, mais aussi leur masse et leurs modes de désintégration. Cela permit à C. Rubbia et S. Van der Meer de les découvrir en 1983 dès la mise en service du faisceau d’antiprotons du C.E.R.N.

Ce grand succès encourage les physiciens à travailler à la «grande unification» de la théorie précédente, de symétrie U(2), et de la théorie semblable, la chromodynamique [facilement unifiée à l’électrodynamique par une symétrie U(3)]. Cela semble possible en étendant la symétrie de jauge des équations de Maxwell et de Dirac au groupe SU(5). Dans cette théorie, le proton est instable (les charges baryoniques b et leptoniques l ne sont donc pas conservées) et a une vie moyenne de 10³² années environ. Depuis 1981, des expériences sont en cours pour vérifier cette prédiction.

Arrivera-t-on a une superunification avec la gravitation? Cette dernière théorie, basée sur des équations différentes, celles d’Einstein, est encore une théorie de jauge. Mais son unification avec les précédentes semble exiger un nouveau concept mathématique appelé «supersymétrie».

Encyclopédie Universelle. 2012.